Concurrent Calculation Of Fibonacci In Elixir
There’s a known formula to evaluate a n Fibonacci term position without iteration or recursion.
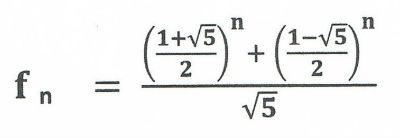
This formula give us a precise approximation:
- Term
n(26) = 121393.00000000009 - Term
n(1200) = 2.7269884455407366e250
Which according with this list, is fine:
- Term
n(26) = 121393 - Term
n(1200) = 272.698844554059974143456202000 × 10²⁷
The actual 1200th term position is 251 digit long, so I’ve posted a equivalent notation here.
A cool (and unrelated) fact is that it uses the Golden Ratio in the calculation (1 + √5) / 2, and what seems a reverse form of it (1 - √5) / 2.
So, the formula I’ve described as:
defmodule FibonacciCalculus do
@golden_n :math.sqrt(5)
def of(n) do
(x_of(n) - y_of(n)) / @golden_n
end
def x_of(n) do
:math.pow((1 + @golden_n) / 2, n)
end
def y_of(n) do
:math.pow((1 - @golden_n) / 2, n)
end
end
By the way, if you haven’t already wondered, after the term 1474 it crashes:
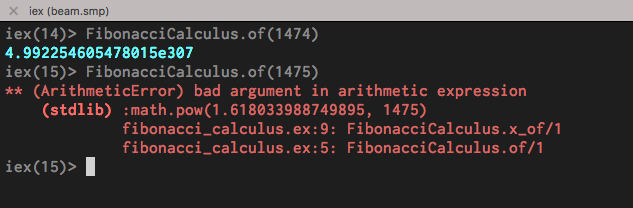
That’s because Erlang’s math module operates only with numbers that can be represented with floating points, and such a big number can’t.
But anyway, my goal here isn’t to calculate Fibonacci at all.
I’m just wanting to see Elixir’s power doing hundreds of those big number calculations at the same time.
I want to give Elixir a sequential integer list, in this case from 1 to 1474, which is the apparent limit. Then ask it to spawn a Erlang process for each one of those elements. Each process should receive the element and return the result of its FibonacciCalculus.of(n), being n the element.
I should end up with a unordered result, as reflect of the concurrent computation.
So, I’ve described the module:
defmodule ConcurrentFibonacci do
def start do
concurrent_map(1..1474, fn(x) ->
"Fibonacci of #{x} is: #{FibonacciCalculus.of(x)}"
end)
end
def concurrent_map(list, func) do
list |> Enum.map(fn e -> spawn(fn ->
IO.puts func.(e)
end) end)
end
end
And the result is beautiful:
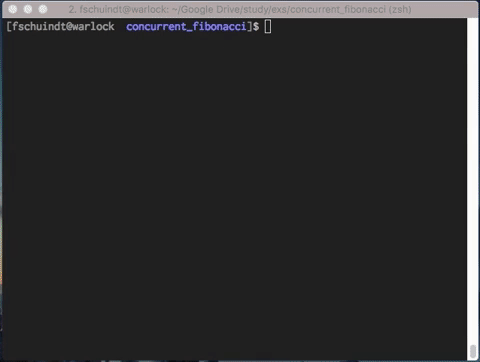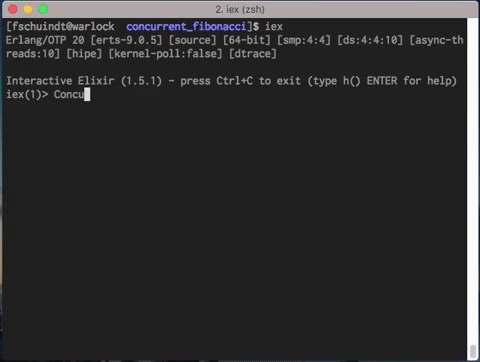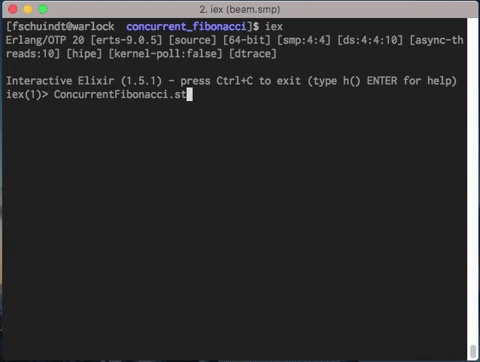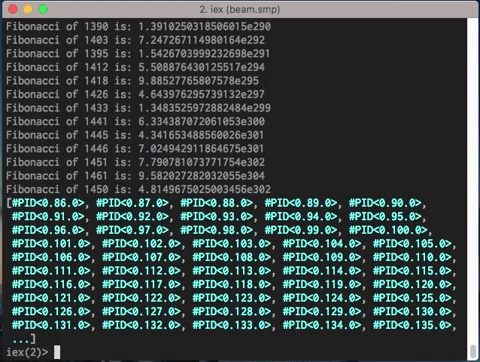
A simple code and it executes more than 1400 concurrent processes in less than a blink of an eye.
Also the unordered result is evident:
[...]
Fibonacci of 1456 is: 8.640108610267577e303
Fibonacci of 1455 is: 5.3398807876359814e303
Fibonacci of 1457 is: 1.397998939790356e304
Fibonacci of 1458 is: 2.262009800817114e304
Fibonacci of 1460 is: 5.922018541424584e304
Fibonacci of 1465 is: 6.567619203443404e305
Fibonacci of 1470 is: 7.28360130920199e306
In an attempt to go deeper, instead of using the 1..1474 list, I’m using the following function:
def list do
Enum.take(Stream.cycle(1..1474), 10_000)
end
This will repeat the 1..1474 list approximately 7x, to result in a list containing 10.000 elements.
Let’s see how it goes:
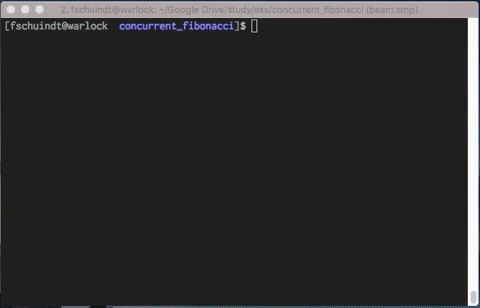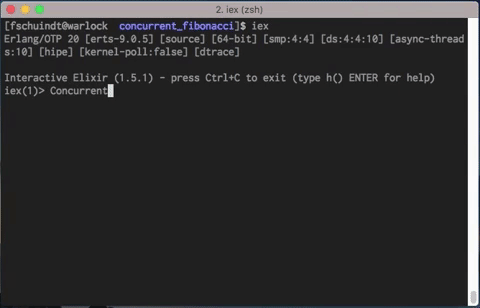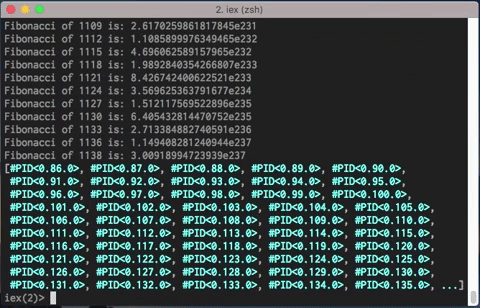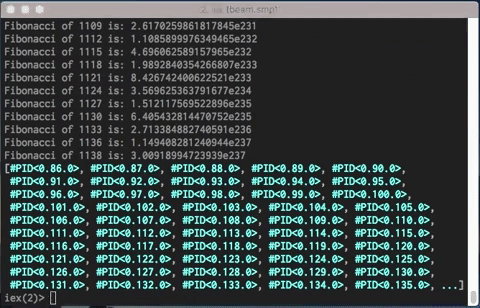
You can see it takes more time, obviously.
But let’s think about it. It’s ten thousand concurrent executions, ten thousand processes.
I have even tested with 100.000 processes, in my 4GB RAM [email protected] notebook it takes 5.47 seconds. One hundred thousand processes in 5 seconds.
I have to say I’m impressed.
I’m about one year playing with Elixir in my spare time, it’s a really fun language, especially if you never programmed functional before.